SPH法における空間離散化その1 (積分形カーネル近似の離散表現)
ここまでのSPH法の近似の説明では,連続関数をカーネル関数を使った積分形で近似するカーネル近似の考え方まで説明しました.ここではじめて粒子を導入し,連続関数を粒子上での値として離散化します.
SPH法ではスカラー関数$\phi$を次のようにカーネル関数を使った領域積分としてカーネル近似しました.
このカーネル近似を使った数値シミュレーションへと準備として,3次元(あるいは2次元)の領域$\Omega$に$\tt N$個の粒子$\boldsymbol{x}_{\tt 1}, \boldsymbol{x}_{\tt 2}, \dots,\boldsymbol{x}_{\tt N}$を配置します. 連続関数のままではシミューションでは扱いにくいため,特に領域積分を離散的な粒子上で定義する値を使って表現していきたいです.そこで,$\tt V_j$は粒子$\boldsymbol{x}_{\tt j}$が代表する体積(粒子体積)とし,つぎのように数値積分することにします.
\begin{align} \phi^{\tt SPH}(\boldsymbol{x}) &= \int_{\Omega} \phi (\boldsymbol{\xi}) w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) {\rm d} \,\boldsymbol{\xi} \tag{19}\\ &\approx \sum_{\tt{j=1}}^{\tt N} {\tt V_j} \phi_{\tt j} w^{\tt SPH}_h (|\boldsymbol{x}_{\tt j}-\boldsymbol{x}|) =: \langle \phi (\boldsymbol{x}) \rangle^{\tt SPH}\tag{20} \end{align}ここで$\phi_{\tt j} $は離散化のために設けた粒子$\tt j$上での関数値$\phi(\boldsymbol{x}_{\tt j})$です.また粒子体積${\tt V_j}$は,領域の体積$|\Omega|$を粒子数$\tt N$で除して${\tt V_j}=|\Omega|/\tt{N}$と定数で与えることにしています.粒子$\tt j$上での物体の密度を密度${\tt \rho_j}$とし,この近似を粒子の質量${\tt m_j}(= {\tt \rho_j V_j})$を使って表わすこともできます.
$$ \langle \phi (\boldsymbol{x}) \rangle^{\tt SPH} = \sum_{\tt j=1}^{\tt N} \frac{\tt m_j}{\tt \rho_j} \, \phi_{\tt j} \, w^{\tt SPH}_h(|\boldsymbol{x}_{\tt j}-\boldsymbol{x}|) \label{sph_phi_basic}\tag{21} $$シミュレーションに向けて導入した離散的な変数(粒子上でのみ定義数量)の添え字は可能な限り,タイプライターフォントを使用する方針とします.また以上の近似の過程($\phi(\boldsymbol x)\xrightarrow{カーネル近似}\phi^{\tt SPH}(\boldsymbol x)\xrightarrow{粒子離散化}\langle \phi(\boldsymbol x) \rangle^{\tt SPH}$)からもわかりますが,SPH法は,「まずは関数$\phi(\boldsymbol x)$を連続関数としてカーネル近似$\phi^{\tt SPH}(\boldsymbol x)$し,さらにカーネル近似における領域積分を近傍の粒子で離散近似$\langle \phi(\boldsymbol x) \rangle^{\tt SPH}$した方法」です. 式\eqref{sph_phi_basic}では,離散近似のために全ての粒子について総和をとっていますが,実際にはカーネル関数のコンパクトサポート条件(6)より,$0<|\boldsymbol{x}-\boldsymbol{x}_{\tt j}|<{h}$を満たす粒子$\boldsymbol{x}_{\tt j}$のみについて総和をとればよいことになります.このように,観測点$\boldsymbol{x}$*3から距離が$h$以内の領域にある粒子の影響のみを考えればよく,その領域$\Omega_h$を点$\boldsymbol{x}$のサポート領域,$h$を影響半径,点$\boldsymbol{x}$のサポート領域内の粒子を点$\boldsymbol{x}$の近傍粒子と呼びます(図2参照).
*3 この点は,注目粒子 i であっても,粒子以外の点であってもよい.
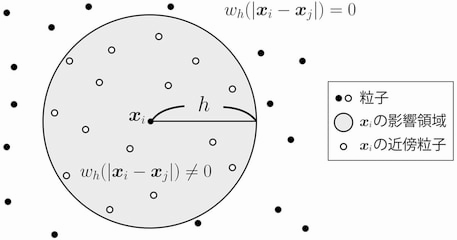
図2 影響領域と近傍粒子の概念図
SPH法における空間離散化その2 (勾配・発散の離散表現)
SPH法による離散近似を使って偏微分方程式を解くには,関数の内挿近似するだけでは十分ではなく,勾配,およびラプラシアンなどの関数の微分に関する離散近似モデルも用意しなくてはいけません. 微分の近似モデルを作るために,ここではまずはカーネル近似する関数として,勾配などの求めたい関数をそのまま代入してみます. スカラー関数の勾配のSPH近似を積分形式にて
\begin{align} ( \nabla \phi (\boldsymbol{x})) ^{\tt SPH0} := \int_{\Omega} \nabla_{\xi} \phi (\boldsymbol{\xi}) \,\, w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) {\rm d} \boldsymbol{\xi} = \int_{\Omega_h} \nabla_{\xi} \phi (\boldsymbol{\xi}) \,\, w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) {\rm d} \boldsymbol{\xi} \label{int_gradient_model}\tag{22} \end{align}と書くことにします*4.最後の等式は,カーネル関数のコンパクトサポート条件より,積分領域を解析領域全体$\Omega$からサポート領域$\Omega_h$(影響半径$h$を半径とする$\boldsymbol x$を中心にした球体)に限定すればよいことを表わしています.また積分変数は$\boldsymbol{\xi}$であり,$\nabla_{\xi} \phi (\boldsymbol{\xi})$は関数$\phi(\boldsymbol {\xi})$の変数$\boldsymbol{\xi}$に関する勾配として表記しています.被積分関数は$\nabla_{\xi} \phi (\boldsymbol{\xi})$と$w^{\tt SPH}_h (|\boldsymbol{x}-\boldsymbol{\xi}|)$の積であることから,積の微分公式から次の関係式へと式変形できます.
*4 このまま近傍粒子での値を使って離散化しようとすると,スカラー関数$\phi$の勾配である3つの成分を新たに未知数として追加することになるので,この段階では積分を粒子の和の形に近似することはしません.
\begin{align} & \nabla_{\xi} \left[ \phi (\boldsymbol{\xi}) w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \right] = \left[ \nabla_{\xi} \phi (\boldsymbol{\xi}) \right] w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) + \phi (\boldsymbol{\xi}) \left[ \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \right] \nonumber \\ & \rightarrow \left[ \nabla_{\xi} \phi (\boldsymbol{\xi}) \right] w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) = \nabla_{\xi} \left[ \phi (\boldsymbol{\xi}) w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \right] – \phi (\boldsymbol{\xi}) \left[ \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \right] \label{chain_rule}\tag{23} \end{align}
式(\ref{chain_rule})を積分形式のSPHカーネル近似の式(\ref{int_gradient_model})に代入し,ガウスの発散定理を使って右辺第1項目の体積積分をサポート領域の境界表面$\Gamma_h$(外向き法線を$\boldsymbol n$とする$\boldsymbol x$を中心とした球の表面)の面積分に変換することで
\begin{align} \left( \nabla \phi (\boldsymbol{x}) \right)^{\tt SPH0} &= \int_{\Omega_h} \nabla_{\xi} \left[ \phi (\boldsymbol{\xi}) w^{\tt SPH}_h (|\boldsymbol{x}-\boldsymbol{\xi}|) \right] {\rm d} \boldsymbol{\xi} – \int_{\Omega_h} \phi (\boldsymbol{\xi}) \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{x}-\boldsymbol{\xi}|) \, {\rm d} \boldsymbol{\xi} \nonumber \\ &= \int_{\Gamma_h} \boldsymbol{n} \left[ \phi (\boldsymbol{\xi}) w^{\tt SPH}_h (|\boldsymbol{x}-\boldsymbol{\xi}|) \right] {\rm d} S – \int_{\Omega_h} \phi (\boldsymbol{\xi}) \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{x}-\boldsymbol{\xi}|) \, {\rm d} \boldsymbol{\xi}\tag{24}\\\ &= – \int_{\Omega_h} \phi (\boldsymbol{\xi}) \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{x}-\boldsymbol{\xi}|) \, {\rm d} \boldsymbol{\xi}\tag{25} \end{align}となります.コンパクトサポート領域の境界$\Gamma_h$上では,コンパクトサポート条件よりカーネル関数はちょうどゼロであるため,第1項目の表面積分の項は消去できます.この積分式は,勾配のSPH近似を与えるための基礎を与える式であり,被積分項が未知関数$\phi(\boldsymbol{\xi})$とカーネル関数の勾配となっています.カーネル関数は観測点$\boldsymbol{x}$からの距離の関数として事前に与えたことから,その勾配も事前に書き下すことができます.また被積分項が未知関数の勾配ではなく,関数値そのものに変換できたので,この領域積分を先ほどと同様に近傍の粒子での値の和として数値的に近似すれば,勾配モデルのひとつ“基礎モデル”$\langle \nabla \phi (\boldsymbol{x}) \rangle^{\tt SPH0}$*5 を与えることができます.
*5 SPH法の基礎であるカーネル近似,粒子離散近似のプロセスを使って勾配をそのまま表現したモデルであるため本書では基礎モデルと呼ぶことにした.
\begin{align} \left( \nabla \phi (\boldsymbol{x}) \right) ^{\tt SPH0} &= – \int_{\Omega_h} \phi (\boldsymbol{\xi}) \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \, {\rm d} \boldsymbol{\xi} \label{grad_simple_int_form}\tag{26}\\ &\approx – \sum_{\tt{j=1}}^{\tt N} {\tt V_j} \phi_{\tt j} \nabla_{\tt j} w^{\tt SPH}_h (|\boldsymbol{x}_{\tt j}-\boldsymbol{x}|) =: \langle \nabla \phi (\boldsymbol{x}) \rangle^{\tt SPH0}\tag{27} \end{align}
ここで,$\nabla_{\tt j}$は$\boldsymbol{x}_{\tt j}$による勾配です.また$\boldsymbol{x}$は任意の点であるので,粒子$\tt i$における関数$\phi$の勾配を与えるためには
\begin{align} \langle \nabla \phi (\boldsymbol{x}_{\tt i}) \rangle^{\tt SPH0} &= – \sum_{\tt{j=1}}^{\tt N} {\tt V_j} \phi_{\tt j} \nabla_{\tt j} w^{\tt SPH}_h (|\boldsymbol{x}_{\tt j}-\boldsymbol{x}_{\tt i}|) \nonumber \\ &= \sum_{\tt{j=1}}^{\tt N} {\tt V_j} \phi_{\tt j} \nabla_{\tt i} w^{\tt SPH}_h (|\boldsymbol{x}_{\tt i}-\boldsymbol{x}_{\tt j}|) \nonumber \\ &= \sum_{\tt{j=1}}^{\tt N} {\tt V_j} \phi_{\tt j} \nabla {\tt w}^{\tt SPH}_{\tt ij} \label{grad_sph1} \tag{28} \end{align}と表現できます.ここで,カーネル関数の偶関数特性$\nabla_{\tt j} w (|\boldsymbol{x}_{\tt j}-\boldsymbol{x}_{\tt i}|) = – \nabla_{\tt i} w (|\boldsymbol{x}_{\tt i}-\boldsymbol{x}_{\tt j}|)$ を使って負の符号を消去し,また記述を簡潔にまとめるために $\nabla {\tt w}^{\tt SPH}_{\tt ij} :=\nabla_{\tt i} w^{\tt SPH}_h (|\boldsymbol{x}_{\tt i}-\boldsymbol{x}_{\tt j}|) $と書くことにしました.この勾配に関する“基礎モデル”$\langle \nabla \phi_{\tt i} \rangle^{\tt SPH0}$によれば,各粒子上での関数$\phi$の勾配は,「近傍粒子$\tt j$の点での関数値$\phi_{\tt j}$に,代表体積$\tt V_j$とカーネル関数の勾配$\nabla {\tt w}^{\tt SPH}_{\tt ij}$を乗じて足し合わせる」ことで評価できます.
勾配の“基礎モデル”$\langle \nabla \phi (\boldsymbol{x}) \rangle^{\tt SPH0}$は勾配モデルのひとつであり,実際にはこのモデルをそのまま使うことはあまりありません.以下では,特に流体解析においては下記に示すテイラー展開に基づく勾配モデル$\langle \nabla \phi (\boldsymbol{x}) \rangle^{\tt SPH}$を誘導します. テイラー展開の2次の項以降を無視すると,
\begin{align} \phi(\boldsymbol{\xi}) – \phi(\boldsymbol x) \approx \frac{ \partial {\phi}} {\partial \boldsymbol \xi} ({\boldsymbol{x}}) \cdot \left [\boldsymbol{\xi}-\boldsymbol{x} \right] \tag{29} \end{align}と近似できるので,この両辺にベクトル$\nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|)$を乗じてサポート領域で積分する*6と,
*6結論からすると右辺が関数$\phi$の勾配を抽出するような操作になっている.
\begin{align} \int_{\Omega_h} [\phi(\boldsymbol{\xi}) -\phi(\boldsymbol{x}) ] \nabla_{\xi} w^{\tt SPH}_h \, {\rm d} \boldsymbol{\xi} \approx \underbrace{ \left [ \int_{\Omega_h} \left [\boldsymbol{\xi}-\boldsymbol{x} \right] \otimes \nabla_{\xi} w^{\tt SPH}_h \, {\rm d} \boldsymbol{\xi} \right] }_{2階のテンソル} \frac{ \partial {\phi}} {\partial \boldsymbol \xi} ({\boldsymbol{x}}) \label{for_gradient_model1}\tag{30} \end{align}
となります.右辺の積分は2階のテンソルとなっていますが*7,この被積分項は積の微分公式を使うことで
*7テンソル積として表わせることの理解が難しい場合には,テンソル積の定義式$\left(\boldsymbol{a} \otimes \boldsymbol{b} \right) \boldsymbol{c}:=\left(\boldsymbol{b} \cdot \boldsymbol{c} \right) \boldsymbol{a} $に戻って考えます. ここでは$\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$はベクトルとします.
\begin{align} &\nabla_{\xi} \otimes ( [\boldsymbol{\xi}-\boldsymbol{x} ] w^{\tt SPH}_h ) = \left [\boldsymbol{\xi}-\boldsymbol{x} \right] \otimes \nabla_{\xi} w^{\tt SPH}_h +\nabla_{\xi} \otimes \left [\boldsymbol{\xi}-\boldsymbol{x} \right] w^{\tt SPH}_h\tag{31} \\ & \rightarrow \left [\boldsymbol{\xi}-\boldsymbol{x} \right] \otimes \nabla_{\xi} w^{\tt SPH}_h = \nabla_{\xi} \otimes ( [\boldsymbol{\xi}-\boldsymbol{x} ] w^{\tt SPH}_h ) – w^{\tt SPH}_h \boldsymbol{1} \label{for_gradient_model2}\tag{32} \end{align}
が成り立ちます.ここで$\boldsymbol{1}$は2階の恒等テンソルです.式(\ref{for_gradient_model2})を式(\ref{for_gradient_model1})に代入し,ガウスの発散定理,カーネル関数のユニティ条件,そしてコンパクトサポート条件を使って整理すると,
\begin{align} \int_{\Omega_h} [\phi(\boldsymbol{\xi}) -\phi(\boldsymbol{x}) ] \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \, {\rm d} \boldsymbol{\xi} & \approx && \underbrace{ \left[ \int_{\Omega_h} \nabla_{\xi} \otimes ( [\boldsymbol{\xi}-\boldsymbol{x} ] w^{\tt SPH}_h ) \, {\rm d} \boldsymbol{\xi} \right. }_{この項に発散定理を適用} – \boldsymbol{1} \underbrace{ \left. \int_{\Omega_h} w^{\tt SPH}_h \, {\rm d} \boldsymbol{\xi} \right] }_{ユニティ条件} \nabla {\phi} (\boldsymbol{x}) \nonumber \\ &=& & \biggl[ \underbrace{ \int_{\Gamma_h} \boldsymbol{n} \otimes ( [ \boldsymbol{\xi} – \boldsymbol{x} ] w^{\tt SPH}_h) \, {\rm d} S }_{=0 (コンパクトサポート条件より)} – \boldsymbol{1} \biggr] \, \nabla {\phi} (\boldsymbol{x}) \tag{33}\\ &=&&- \nabla {\phi} (\boldsymbol{x}) \tag{34} \end{align}となります.あとは,領域積分を近傍粒子により離散近似することで,これがテイラー展開に基づく勾配モデルとなります.まずはカーネル近似は
\begin{align} \nabla {\phi} (\boldsymbol{x}) \approx (\nabla {\phi} (\boldsymbol{x}) )^{\tt SPH} := – \int_{\Omega^h} [\phi(\boldsymbol{\xi}) -\phi(\boldsymbol{x}) ] \nabla_{\xi} w^{\tt SPH}_h (|\boldsymbol{\xi}-\boldsymbol{x}|) \, {\rm d} \boldsymbol{\xi} \label{grad_sa_int_form}\tag{35} \end{align}として与えられ,これを粒子離散近似することで
\begin{align} \langle \nabla {\phi} (\boldsymbol{x}) \rangle^{\tt SPH} := -\sum_{\tt j}^{\tt N} \frac{\tt m_j}{\rho_{\tt j}} \left[ \phi(\boldsymbol x_{\tt j}) – \phi(\boldsymbol x) \right] \nabla_{\tt j} w^{\tt SPH}_h(|\boldsymbol x_{\tt j}-\boldsymbol{x}|) \label{sph_approx_gradient}\tag{36} \end{align}を得ます.先の“基礎モデル”と対比するため,上式(\ref{sph_approx_gradient})を“差モデル”として参照することにします. ここでも式の整理のため,$\nabla {\tt w}^{\tt SPH}_{\tt ij} =-\nabla_{\tt j} w^{\tt SPH}_h (|\boldsymbol{x}_{\tt j}-\boldsymbol{x}_{\tt i}|)$として負の符号をなくし, 粒子$\tt i$における関数$\phi$の勾配モデルを整理します.
\begin{align} \langle \nabla {\phi}_{\tt i} \rangle^{\tt SPH} := \langle \nabla {\phi} (\boldsymbol x_{\tt i}) \rangle^{\tt SPH} = \sum_{\tt j}^{\tt N} \frac{\tt m_j}{\rho_{\tt j}} (\phi_{\tt j} – \phi_{\tt i} ) \nabla {\tt w}^ {\tt SPH}_{\tt ij} \tag{37} \end{align}勾配の“差モデル”$\langle \nabla {\phi}_{\tt i} \rangle^{\tt SPH}$によれば,各点で関数$\phi$の勾配は,「注目粒子$\tt i$での関数値$\phi_{\tt i}$に対する近傍粒子$\tt j$の点での関数値$\phi_{\tt j}$の差に,代表体積$\tt V_j$とカーネル関数の勾配ベクトル$\nabla {\tt w}^{\tt SPH}_{\tt ij}$を乗じて足し合わせる」ことで評価できる.先に紹介した基礎モデルとの差は,離散近似を導入する前のカーネル近似の差(式(\ref{grad_simple_int_form})と式(\ref{grad_sa_int_form})の違い)から生じたものであり,領域積分の精度の差ではないことがわかります.つまり,勾配のカーネル近似の段階で,$(\nabla {\phi})^{\tt SPH0}$と$(\nabla {\phi})^{\tt SPH}$に差が生じており,あとは内挿近似でも使った粒子離散近似(被積分項の関数値に粒子体積をかけて総和をとることで領域積分を近似)でモデルを与えています.
著者ご紹介

九州大学大学院 工学研究院
社会基盤部門 准教授
浅井 光輝 先生
プロフィールを見る
2003年
東北大学大学院工学研究科 博士(工学)
2003年
オハイオ州立大学機械工学科 博士研究員
2005年
立命館大学マイクロ機械システム工学科 助手
2007年
九州大学大学院工学研究院社会基盤部門 准教授
